第一题：进制转换 2022 九进制转十进制 为 1475 不解释

第二题：用手数 ，4个。

该题有歧义，012X 不算顺子日期就离谱

第三题：刷题统计

考试代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<iostream>
using namespace std;
long long a,b,n;
int total;
bool flag=false;
int main(void)
{  
	cin>>a>>b>>n;
	while(1){
        if(!flag)
            for(int i=1;i<=5;i++)
            {
                total++; //天数
                n=n-a;
                if(n<=0){
                    flag=true;
                    break;
                }
            }

        if(!flag){
            for(int i=1;i<=2;i++)
            {   
                total++;
                n=n-b;
                if(n<=0){
                    flag=true;
                    break;
                }
            }

        }
        if(flag) break;
    }
	cout<<total;
	
}

得了80分，剩余时间超限。

正解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<iostream>
using namespace std;
int main(void)
{
	long long a,b,n;
	cin>>a>>b>>n;
	long  day_7 = a*5+b*2;
	long  sumday = (n /day_7)*7;
	n=n%day_7;
	
	if(n>a*5) {
		sumday += 5;
		n-=a*5;
		if(n>b) sumday+=2;
		else sumday+=1;
	}
	else {
		sumday += n/a;
		if(n%a>0){
			sumday+=1;
		}
	}
	cout<<sumday;
}

总结：

  1. for 循环多了会超限。

  2. 这题解开始都是int类型，我觉得 数据范围是 1~1081 ，怎么也不会超限。

    结果还就是超限了。乘法很可怕，long long有奇效。

第四题 修剪灌木

枚举

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<bits/stdc++.h>
using namespace std;
long long  tree[10100][10100]={0}; //记录每一天轨迹 
long long  maxnum[10100]={0}; // 记录每一位 的 最大值 
int tail=0;      //记录 爱丽丝 坎位置 
	int N;    //多少棵 
bool flag=true;
bool findx(int locate)     //是否重复？  locate = y值 
{  bool ok;
	for(int i=1;i<locate;i++)
	{	ok=1;
		for(int k=1;k<=N;k++){
		if(tree[locate][k]!=tree[i][k]) ok=0;
	    }
		if(ok==1)  return true;
	}
    return false;
}
int main()
{  	int y=1;
	cin>>N;
	while(1){
		
		if(flag) tail++;   //flag 决定 正向进行 反向进行 
		else tail--;   //一轮一天 
	    if(tail==N) flag=false; //到头了 
	    if(tail==0) {flag=true; tail=2;} //回来了 
		for(int i=1;i<=N;i++)   //  这一轮，每棵树 长1cm 
		{
		    tree[y][i]=tree[y-1][i]+1;
			if(tree[y][i]>maxnum[i]) maxnum[i]=tree[y][i];	//最大值 记录 
	    }
	    tree[y][tail]=0;  //让砍位 为0 
	
	    if(y>1&&findx(y)) break; //寻找重复点 （重复后结束循环） 
	    else y++; //下一天！
	}
	
	for(int i=1;i<=N;i++)
	{
		cout<<maxnum[i];
		if(i!=N) cout<<endl;
	}
	return 0;
}

这个代码输出的是正确答案。但是运行超限，很伤。

如果把long long 改成 int ，能得这道题一半的分！

面向规律:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
#include<vector>
using namespace std;
int main(void)
{
	vector<long long> v;
	bool flag;
	long long n;cin>>n;
	if(n%2==0) {
		flag =true;
		v.push_back(n);} //奇数偶数 
	else {
		flag = false;
		v.push_back(n-1);}
	
	int mid_num = *v.begin();
	if(flag) v.push_back(mid_num); //偶数就多加一个 
	
	for(int i =1;i<=(n-1)/2;i++){
		v.push_back(mid_num+2*i);
	}
	
	//倒着输出一遍 正着输出一遍
	for(vector<long long>::reverse_iterator rit = v.rbegin();rit!=v.rend();rit++){
		cout<<*rit<<endl;
	} 
	for(vector<long long>::iterator it = v.begin();it!=v.end();it++){
		if(*it!=mid_num) cout<<*it<<endl;
	} 
	
}

面向规律2.0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<iostream>
#include<vector>
using namespace std;

vector<int> getmaxdata(int N){
	vector<int> ret(N + 1, 0);
	for(int i = 1; i <= N; i++){
		ret[i] = 2 * (N - i);
	}
	for(int i = 0; i < N / 2; i++){
		ret[N - i] = ret[i + 1];
	} 
	return ret;
}

int main(){
	
	int N;
	cin >> N;
	vector<int> ans = getmaxdata(N);
	for(int i = 1; i <= N; i++){
		cout << ans[i];
		if(i != N){
			cout << endl;
		}
	}
	return 0;
}

总结：不要着急写题，在纸上跟着示例模拟一下过程，可能会有数学规律。发现规律后解题会出乎意料的简单。

第五题 X进制数

  • 位数少的数高位补0，然后在进制上 跟随位数多的数

比如 A是 123 B是 4567

A → 0123 ，进制上和4567一样

  • 每一位上的数都是其所有低位数的累计。

比如 123 的 X进制 ，第一位 十进制 ，第二位八进制，第三位五进制

则 123 = 1 * 8 * 5+ 2 * 5 + 3

如果 进制分别为 a b c ，则

123 = 1 * b * c + 2 * c + 3

代码：

1

第六题 统计子矩阵

DFS 骗分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<bits/stdc++.h>
using namespace std;
int mmap[510][1010];
int K,N,M;
long long total;
void dfs(int tx,int ty,int h,int w)
{   
    if(tx+h>=N||ty+w>=M) return ;
    
    int num=0;
    for(int k=0;k<=h;k++){
    	for(int j=0;j<=w;j++){
    		num+=mmap[tx+k][ty+j];
    	}
    }
	if(num<=K){
		total++;
		dfs(tx,ty,h+1,w);
		dfs(tx,ty,h,w+1);
	}
	else return;
}
int main(void)
{
    cin>>N>>M>>K;
    for(int x=0;x<N;x++){   //赋值 
    	for(int y=0;y<M;y++){
    		cin>>mmap[x][y];
    	}
    } 
    
    for(int x=0;x<N;x++){   
    	for(int y=0;y<M;y++){
    		dfs(x,y,0,0);
    	}
    } 
    cout<<total;
}

针对列的一维前缀和 + 针对行的滑动窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<iostream>
using namespace std;

int num[550][550];

int main(void)
{
	long long int total=0;
	int N,M;	
	int K;
	cin>>N>>M>>K;
	int temp;
	for(int i=1;i<=N;i++){
		for(int j=1;j<=M;j++){
			cin>>temp;
			num[i][j] = temp;
			num[i][j]+=num[i-1][j];
		}
	}
	//纵向拉伸 
	for(int i=1; i<=N; i++) //纵向每个点作为初始点 
	{
		for(int	j=i;j<=N; j++)  
		{
			//横向拉伸                                              
			for(int left=1,right=1,sum=0; right<=M; right++)      //右扩
			{
				sum+=num[j][right]-num[i-1][right]; //加右扩值 
				while (sum>K)                                    //左缩              
				{
					sum-=num[j][left]-num[i-1][left];  //减左缩值 
					left++;
				}
				total+=right-left+1;  //每次都右扩，直到满足K条件。不满足即为0 
			}                         
		}
	}
	cout<<total;	
		
}	
/*

3 4 10
1 2 3 4
5 6 7 8
9 10 11 12

*/

总结：

  • 学到了前缀和（也就是打表）

  • 数据类型选择：今天我写了三道题，都因为 int , short , long long int 这种类型的差别，丢了分。引以为戒。太大了容易爆，太小了有些大数输出不出来。
    创数组也是这样，长度和数据大小都要考虑。

第七题

典型DP

两个思路

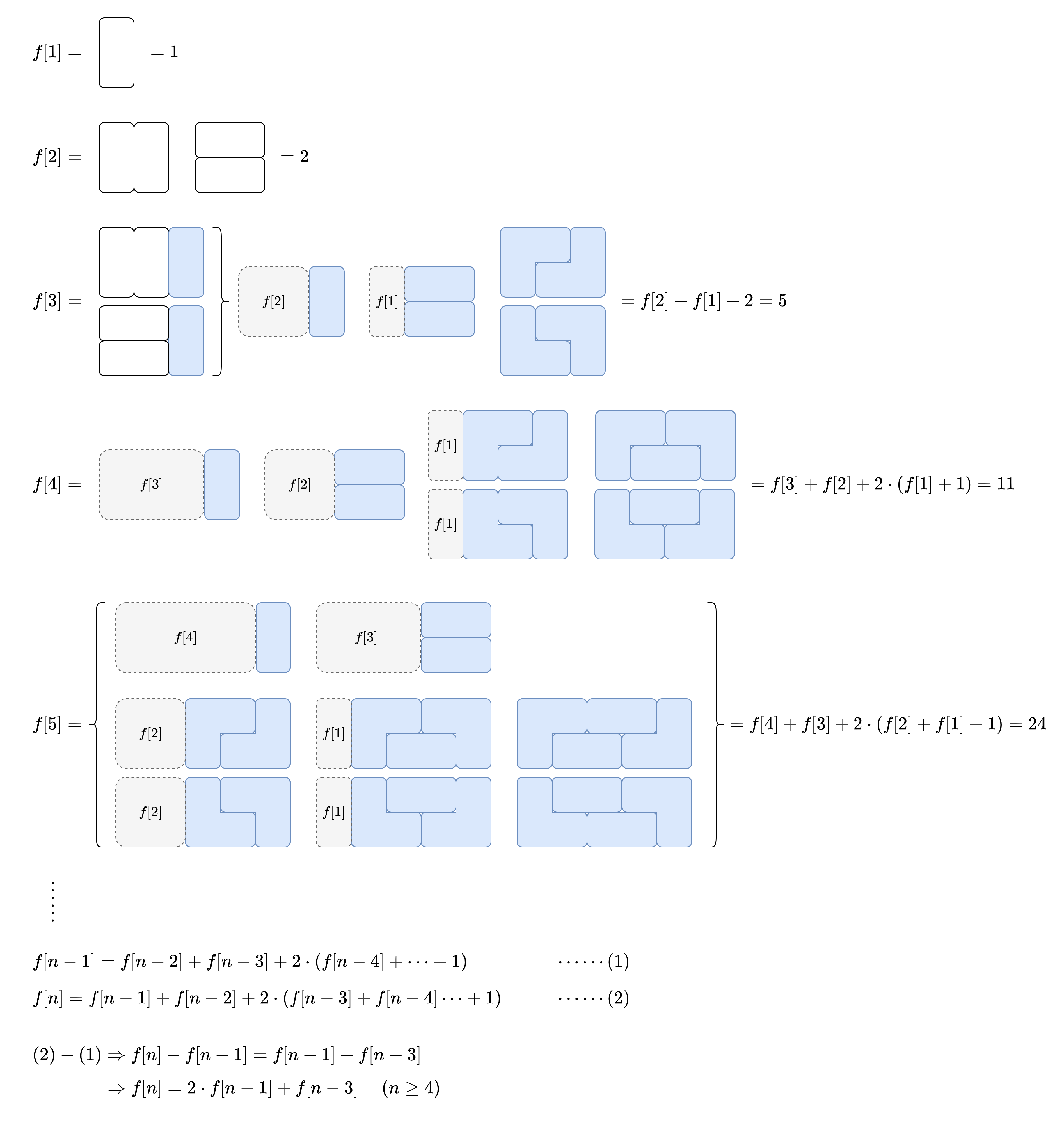
  1. 考虑2xN和积木的拼接方式，有矩形 和 矩形后多一个方块儿 两种拼接情况出现。

    上方块和下方块合并的方式：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    #include<stdio.h>
    #define mod 1000000007
    long int a[10000001][2];
    int main()
    {
         int n;
        a[1][0]=1,a[2][0]=2,a[1][1]=2,a[2][1]=4;
        scanf("%d",&n);
        if(n==1)printf("1");
        else if(n==2)printf("2");
        else {
            for(int i=3;i<=n;i++){
                a[i][0]=(a[i-2][0]+a[i-2][1]+a[i-1][0])%mod;
                a[i][1]=(a[i-1][0]*2+a[i-1][1])%mod;
            }
            printf("%ld",a[n][0]%mod);
        }
        return 0;
    }

    上下方块分明的方式

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    class Solution {
    public:
        int numTilings(int n) {
            long long dp[1005][3]={0};
            int mod=1e9+7;
            dp[0][0]=1;dp[0][1]=1;dp[0][2]=1;
            dp[1][0]=1;dp[1][1]=0;dp[1][2]=0;
            for(int i=2;i<=n;i++)
            {
                dp[i][0]=(dp[i-1][0]+dp[i-1][1]+dp[i-1][2]+dp[i-2][0])%mod;
                dp[i][1]=(dp[i-2][0]+dp[i-1][2])%mod;
                dp[i][2]=(dp[i-2][0]+dp[i-1][1])%mod;
            }
            return dp[n][0];
        }
    };

  2. 数学规律找 Fn

    image

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    class Solution {
        const int MOD = 1e9 + 7;
    public:
        int numTilings(int n) {
            if (n == 1) return 1;
            long f[n + 1];
            f[0] = f[1] = 1;
            f[2] = 2;
            for (int i = 3; i <= n; ++i)
                f[i] = (f[i - 1] * 2 + f[i - 3]) % MOD;
            return f[n];
        }
    };

第八题 扫雷

暴力()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<bits/stdc++.h> 
#include<queue>
using namespace std;
int n,m;
int total;
class node{
public:
	int x,y;
	int r;
	bool flag; //引爆标志
	
	node(int xx,int yy,int rr,int ff):x(xx),y(yy),r(rr),flag(ff){};	

};

vector<node> q1; //雷 
queue<node> q2; //排雷
int main(void)
{   
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {   int x,y,r;cin>>x>>y>>r;
    	q1.push_back(node(x,y,r,0));
    }
    for(int i=1;i<=m;i++)
    {   int x,y,r;cin>>x>>y>>r;
    	q2.push(node(x,y,r,0));
    }
    
    while(!q2.empty())
    {
    	int tx=q2.front().x;
    	int ty=q2.front().y;
		int tr=q2.front().r;
		for(int i=0;i<n;i++)
		{
			if(tr>=sqrt((tx-q1[i].x)*(tx-q1[i].x)+(((ty-q1[i].y))*((ty-q1[i].y)))))
			{
				q1[i].flag=true;
				total++;
			}
		}
    	q2.pop();
    }
    for(int i=0;i<n;i++)
    {
    	if(q1[i].flag){
    		for(int k=i;k<n;k++){
                int tx=q1[k].x;
                int ty=q1[k].y;
	    		if(!q1[k].flag&&q1[i].r>=sqrt((tx-q1[i].x)*(tx-q1[i].x)+((ty-q1[i].y)*(ty-q1[i].y))))
				{
					q1[k].flag=true;
					total++;
				}	
    	  }
		}
    	
    }
   cout<<total;

}

快来参与讨论吧~