反转链表

不要跳进递归，而是利用明确的定义来实现算法逻辑。你的脑袋有几个栈啊！

  • 基本上，所有的递归问题都可以用递推公式来表示。有了这个递推公式，我们就可以很轻松地将它改为递归代码。。所以，遇到递归不要怕，先想递推公式。

  • 递归是一种关于某个重复动作(完成重复性的功能)的形式化描述。具体点讲，如果一个问题 A 可以分解为若干子问题 B、C、D，你可以假设子问题 B、C、D 已经解决，在此基础上思考如何解决问题 A。

  • 将问题抽象化，可以将问题抽象为f(n)（或者其他的数学符号）, 然后用f(n)代表欲求的问题，然后去发现和子问题（比如f(n-1)）的递推关系！（这一点在写动态规划的时候特别有用，其实动态规划就是记忆化的递归！）

  • 递归函数是带语义的，但是记住一个递归函数只有一个语义，如果在写递归函数实现的时候，发现出现了多个语义，需要对新出现的语义重新定义一个函数！

作者：Chuancey
链接：https://leetcode.cn/problems/fan-zhuan-lian-biao-lcof/solution/kan-bu-dong-di->gui-de-kan-guo-lai-xi-wan-1akq/

进入正题：反转链表题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        if(left==1) return reverselist(head,right);

        head->next = reverseBetween(head->next,left-1,right-1);
        return head;
    }
    ListNode* reverselist(ListNode* head,int n)
    {
        if(n==1){
            last2 = head->next;
            return head;
        }
        ListNode* last = reverselist(head->next,n-1);
        head->next->next = head;
        head->next = last2;
        return last;
        
    }
private: ListNode* last2;
};

反转链表的思路是 全反转 → 从1到n 的反转 → 从m到n的反转

全反转的代码：

1
2
3
4
5
6
7
8
9
reverse(ListNode* head){
    if(head==NULL||head->next==NULL){
        return head;
    }
    ListNode* last = reverse(head->next);
    head->next->next = head;
    head->next = NULL ;//这里是区分反转链表范围的关键点
    return last; //返回“头结点”
}

1到n：

1
2
3
4
5
6
7
8
9
10
11
12
ListNode* last2;
reverseN(ListNode* head, int n)
{
    if(n==1){
        last2 = head->next;
        return head;
    }
    ListNode* last = reverseN(head->next,n-1);
    head->next->next = head;
    head->next = last2;     
    return last;
}

和全反转相比，要区分 last: 反转的头结点(原最后结点) , last2:反转的尾结点的next(原起始结点的next)

1664096225632

m到n：照顾头结点，

1
2
3
4
5
6
ListNode* reverseBetween(ListNode* head, int left, int right) {
    if(left==1) return reverseN(head,right) //老样子了      让left定位为“1”
    //注意 reverseN 和 reverseBetween 的区别
    head->next = reverseBetween(head->next,left-1,right-1); //正好在m点接受 “1”到 n
    return head;
}

拓展：
同样的问题有个迭代的法子：

全反转：

1
2
3
4
5
6
7
8
9
10
11
ListNode* prev = nullptr;
ListNode* curr = head;
while(curr)
{
    ListNode* n = curr->next; //记录点位
    curr->next = prev;
    //分成两部分。
    prev = curr;
    curr = next;
}
return prev;

mn反转（头插法）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    ListNode *reverseBetween(ListNode *head, int left, int right) {
        // 设置 dummyNode 是这一类问题的一般做法
        ListNode *dummyNode = new ListNode(-1);
        dummyNode->next = head;
        ListNode *pre = dummyNode;
        for (int i = 0; i < left - 1; i++) {
            pre = pre->next;
        }
        ListNode *cur = pre->next;
        ListNode *next;
        for (int i = 0; i < right - left; i++) {
            next = cur->next;
            cur->next = next->next;
            next->next = pre->next;
            pre->next = next;
        }
        return dummyNode->next;
    }
};

1664098492746

此时把线拉直就是变化后的效果。

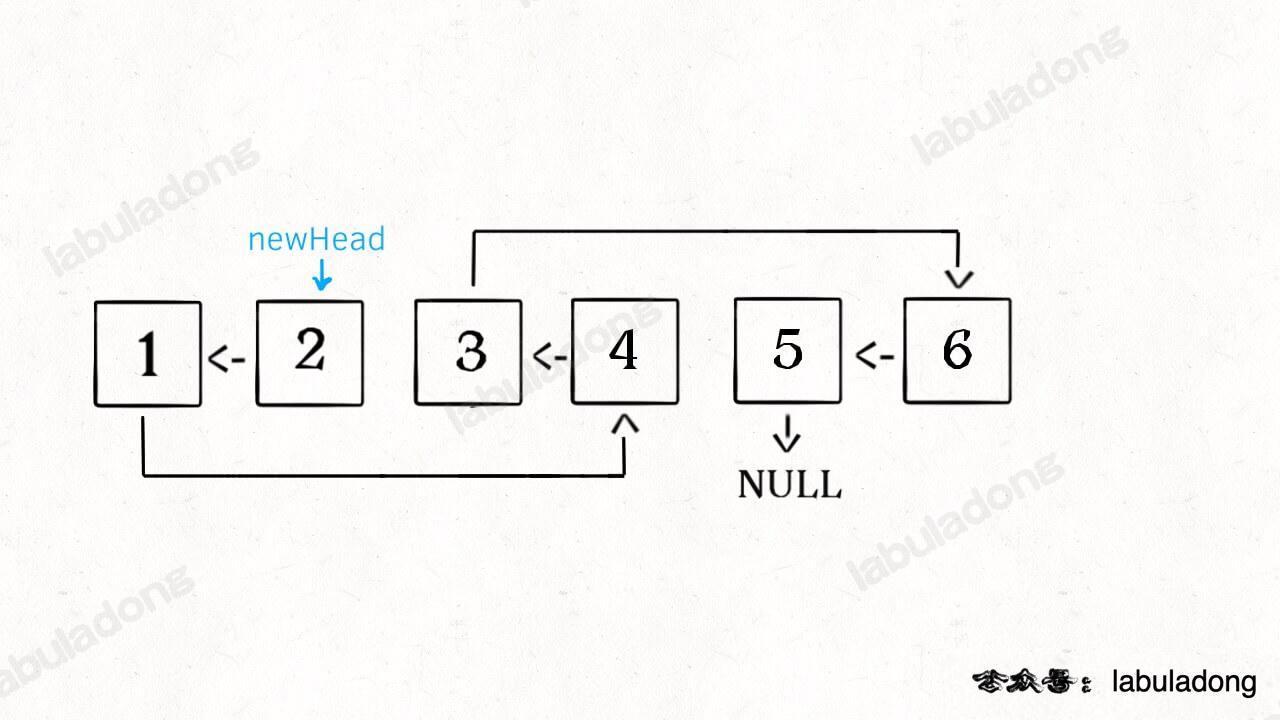
反转一组固定长度为K的链表

img 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
ListNode* reverseKGroup(ListNode* head, int k) {
    if(!head) return head;
    ListNode* a = head;
    ListNode* b = head;
    for(int i=0;i<k;i++) //扩展b顺便检查
    {
        if(!b) return a;
        b=b->next;
    }
    ListNode* newHead = reverse(a,b);  //newHead是反转后头结点
    a->next = reverseKGroup(b,k);  //a 是反转后尾结点
    return newHead;
    
}
ListNode* reverse(ListNode* a,ListNode* b)  //反转a到b 
{
    ListNode* cur = a;
    ListNode* pre = NULL;
    while(cur!=b)
    {
        ListNode* n = cur->next;
        cur->next = pre;
        pre = cur;
        cur = n;
    }
    return pre;        //reverse返回的是反转后的头结点
}

判断回文链表

思路一：

链表不能直接走，但可以借助后序遍历的思路，左指针为头结点，后序遍历比较

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool isPalindrome(ListNode* head) {
        left = head;
        return traverse(head);
    }
    bool traverse(ListNode* right)  //后序遍历比较
    {
        if(right == NULL) return true;
        bool res = traverse(right->next);
        res = res&&(left->val == right->val);
        left = left->next;
        return res;
    }
private:
    ListNode* left ;   //左指针
};

思路二：反转链表后模仿双指针（从中间向两边）

三步走：

  1. 找到中间结点：快慢指针
  2. 反转链表
  3. 前半部分和后半部分逐个对比。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    bool isPalindrome(ListNode* head) {
        ListNode* left = head;
        //no.1
        ListNode* right = midpointer(head); 
        //no.2
        right = reverse(right);
        //no.3
        return compnode(left,right);
        
    }
    //1. 找到中间结点：快慢指针。
    ListNode* midpointer(ListNode* head){
        ListNode* slow = head;
        ListNode* fast = head;
        while(fast!=NULL&&fast->next!=NULL)
        {
            slow = slow->next;
            fast = fast->next->next;
        }
        if(fast!=NULL) slow=slow->next;
        return slow;
    }
    //2.反转后半部分链表。
    ListNode* reverse(ListNode* head){
        ListNode* pre = NULL;
        ListNode* cur = head;
        while(cur!=NULL)
        {
            ListNode* n = cur->next;
            cur->next = pre;
            pre = cur;
            cur = n;
        }
        return pre;
    }
    //3.前半部分和后半部分逐个对比。
    bool compnode(ListNode* left,ListNode* right){
    while(right!=NULL)
    {
        if(left->val!=right->val) return false;
        left = left->next;
        right = right->next;
    }
    return true;
    }
};

快来参与讨论吧~